链表

链表的题目，主要有两大要点，其一是思路，其二是编码。

LeetCode206:反转一个单链表

维护三个指针，prev, current, next，从前往后，以此反转

public ListNode reverseList(ListNode head) {
    ListNode prev = null;
    ListNode current = head;
    
    while (current != null) {
        ListNode next = current.next;
        current.next = prev;
        prev = current;
        current = next;
    }
    
    return prev;
}

LeetCode24:两两交换链表中的节点

思路1：维护三个指针，prev、next1、next2，以prev为遍历中心，操作prev、next1、next2、next3的指针。

public ListNode swapPairs(ListNode head) {
    ListNode dummy = new ListNode(0);
    dummy.next = head;
    
    ListNode prev = dummy;
    while (prev.next != null && prev.next.next != null) {
        ListNode next1 = prev.next;
        ListNode next2 = next1.next;
        ListNode next3 = next2.next;
        
        prev.next = next2;
        next1.next = next3;
        next2.next =next1;
        
        prev = next1;
    }
    return dummy.next;
}

思路2：递归反转，维护next1，next2两个指针

public ListNode swapPairs(ListNode head) {
    if (head == null || head.next == null) {
        return head;
    }
    
    ListNode next1 = head.next;
    ListNode next2 = next1.next;
    next1.next = head;
    head.next = swapPairs(next2);
    return next1;
}

LeetCode160:相交链表

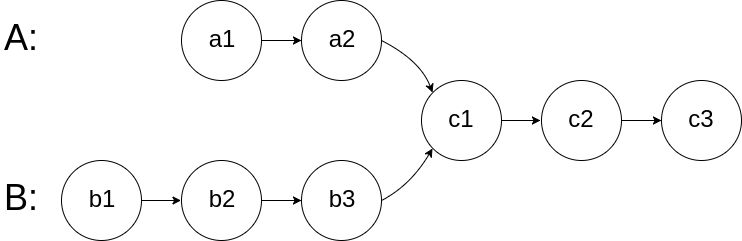
如上图，分为三部分 a\b\c。解题思想就是 a+c+b = b+c+a

也就是两个链表遍历，结束时从另一个链表的头继续遍历，直到相遇

public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    ListNode nodeA = headA, nodeB = headB;
    
    while (nodeA != nodeB) {
        nodeA = nodeA == null ? headB : nodeA.next;
        nodeB = nodeB == null ? headA : nodeB.next;
    }
    return nodeA;
}

LeetCode141:判断链表是否有环

思路1：Set存储遇到的每一个ListNode，从前往后遍历，直到结束或者遇到Set中存在的，返回。

思路2：快慢指针，龟兔赛跑。慢指针每次向前一步，快指针每次两步，如果有环，必然相遇！

public boolean hasCycle(ListNode head) {
    ListNode slow = head, fast = head;
    while (slow != null && fast != null) {
        slow = slow.next;
        fast = fast.next;
        if (fast == null) {
            return false;
        }
        fast = fast.next;
        
        if (slow == fast) {
            return true;
        }
    }
    return false;
}

LeetCode142:求链表中环的起点

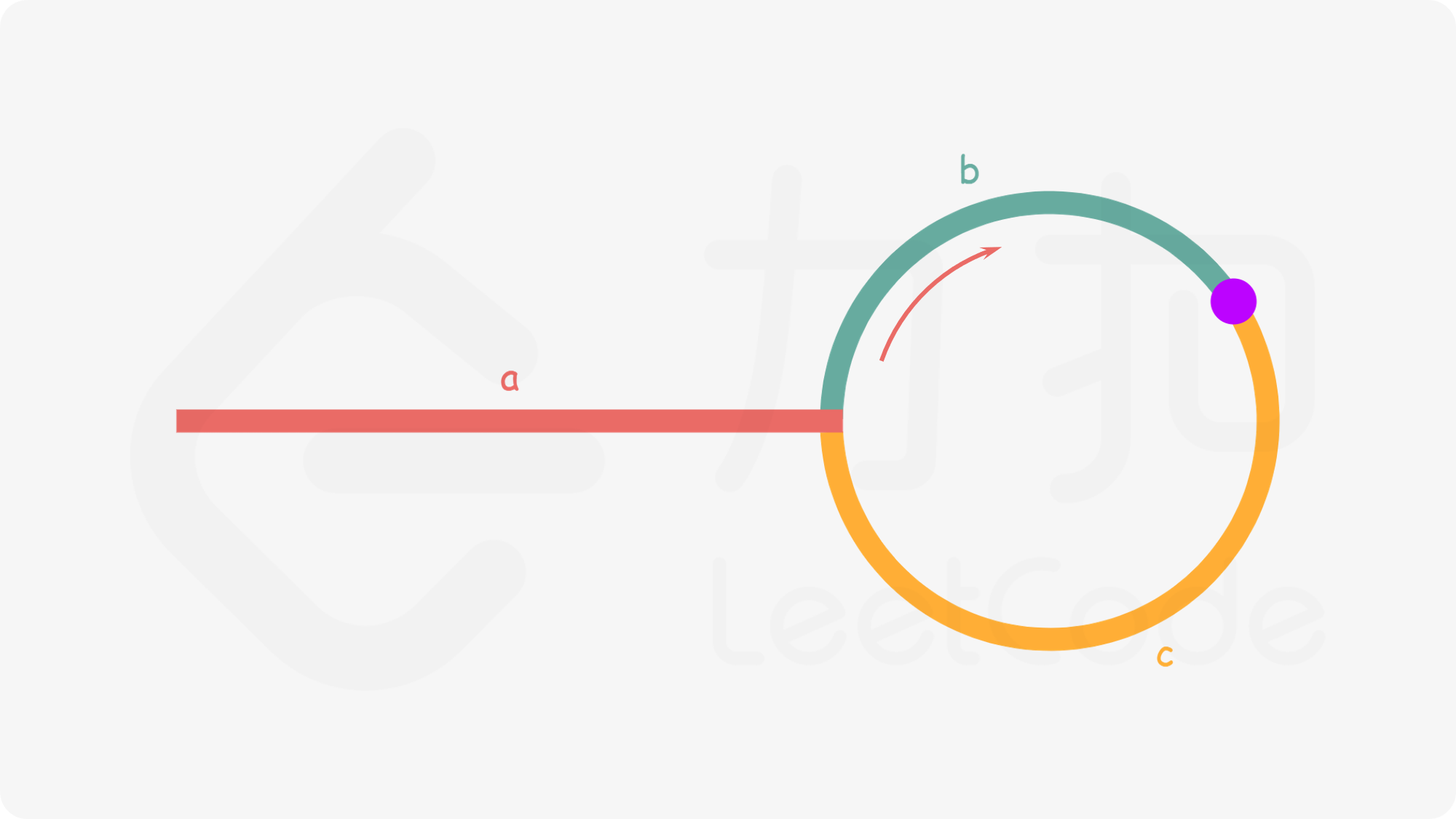
求是否有环，用到了快慢指针，本题依然使用快慢指针。如上图所示，分为三部分。当快慢指针首次相遇于紫色点处时,

满指针走了a+b，快指针走了a+b+c+b，又因为快指针走的路长为慢指针的两倍。所以得出：

2(a+b) = a+b+c+b => a = c

so，首次相遇时，再加一个指针pointer指向链表的起点，慢指针走一步，pointer走一步，相遇时，就是环的起点！

public ListNode detectCycle(ListNode head) {
    ListNode slow = head, fast = head;
    
    while (slow != null && fast != null) {
        slow = slow.next;
        fast = fast.next;
        if (fast == null) {
            return null; // 无环返回null
        }
        
        fast = fast.next;
        
        if (slow == fast) {
            // 快慢指针相遇，新建指针从链表head开始,知道与慢指针相遇
            ListNode pointer = head;
            while (pointer != slow) {
                pointer = pointer.next;
                slow = slow.next;
            }
            return slow;
        }
    }
    return null;
}

LeetCode234:回文链表

思路简单：快慢指针，慢指针移动的时候反转链表，并维护prev指针。快指针先行，遍历到null的时候说明慢指针到了中间。然后slow和prev向两边开始对比。

注意点：节点数为奇数时，慢指针刚好在中间；节点数为偶数时，慢指针为后一部分的第一个节点。

根据fast为null还是fast后面的第一个节点为null，区分节点总数是奇数还是偶数。

public boolean isPalindrome(ListNode head) {
    ListNode slow = head, fast = head;
    
    ListNode prev = null;
    boolean isOdd = false; // 节点总数是否是奇数个
    
    while (fast != null) {
        fast = fast.next;
        if (fast == null) {
            // fast下一个节点为null,说明节点总数是奇数
            isOdd = true;
            break;
        }
        fast = fast.next;
        
        ListNode next = slow.next;
        slow.next = prev;
        prev = slow;
        slow = next;
    }
    
    ListNode leftPointer = prev;
    ListNode rightPointer = isOdd ? slow.next : slow;
    while (leftPointer != null && rightPointer != null) {
        if (leftPointer.val != rightPointer.val) {
            return false;
        }
        leftPointer = leftPointer.next;
        rightPointer = rightPointer.next;
    }
    return true;
}

思路2：递归判断是否回文。利用栈的特性，维护一个前置指针，递归栈里存放后置指针，递归到最深层时，不断弹栈，前置指针也不断后移，两相比较。这种不好，无法预知栈的深度！此处仅作为一种解题思想。

ListNode front;
public boolean isPalindrome(ListNode head) {
    front = head;
    return checkPalindrome(head);
}

private boolean checkPalindrome(ListNode node) {
    if (node != null) {
        if (!checkPalindrome(node.next)) {
            return false;
        }
        if (node.val != front.val) {
            return false;
        }
        front = front.next;
    }
    return true;
}