Leetcode 307. 区域和检索 - 数组可修改

发表于 | 分类于 | 阅读次数：

题目

给你一个数组 nums ，请你完成两类查询，其中一类查询要求更新数组下标对应的值，另一类查询要求返回数组中某个范围内元素的总和。

实现 NumArray 类：

  • NumArray(int[] nums) 用整数数组 nums 初始化对象
  • void update(int index, int val) 将 nums[index] 的值更新为 val
  • int sumRange(int left, int right) 返回子数组 nums[left, right] 的总和（即，nums[left] + nums[left + 1], …, nums[right]）

示例：

输入：
[“NumArray”, “sumRange”, “update”, “sumRange”]
[[[1, 3, 5]], [0, 2], [1, 2], [0, 2]]
输出：
[null, 9, null, 8]

解释：
NumArray numArray = new NumArray([1, 3, 5]);
numArray.sumRange(0, 2); // 返回 9 ，sum([1,3,5]) = 9
numArray.update(1, 2); // nums = [1,2,5]
numArray.sumRange(0, 2); // 返回 8 ，sum([1,2,5]) = 8

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/range-sum-query-mutable
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

代码

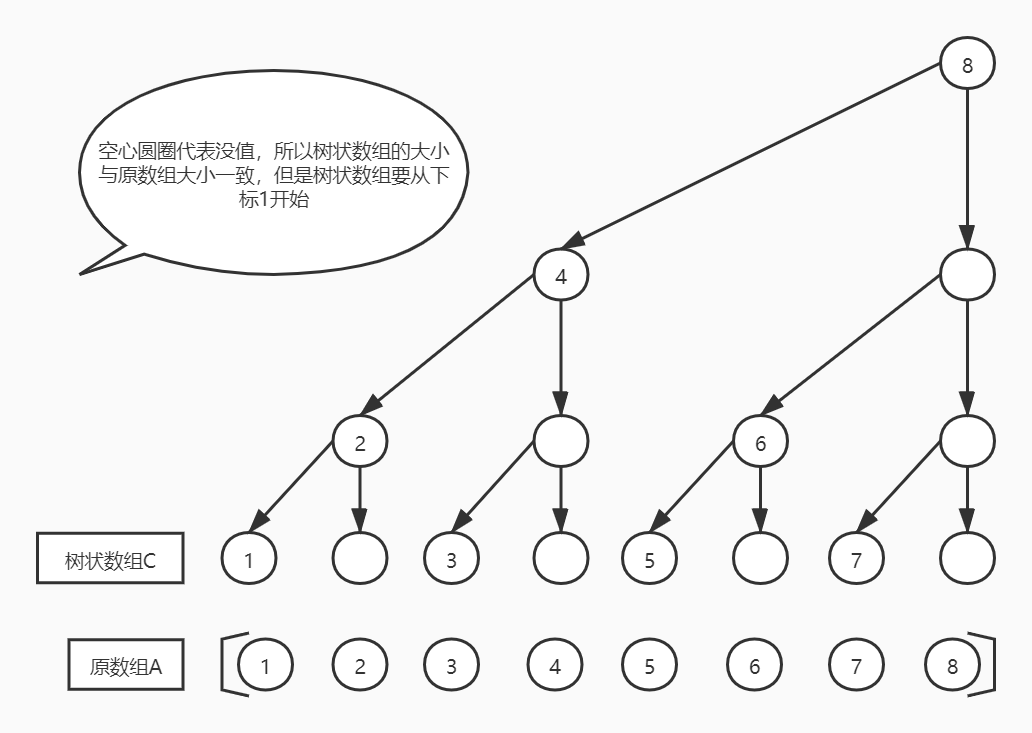
树状数组解题

  • avatar
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class NumArray {
    int[] nums;

    int[] tree;

    int n;

    public NumArray(int[] nums) {
        this.nums = nums;
        this.n = nums.length;
        this.tree = new int[n + 1];
        for (int i = 0; i < n; i++) {
            add(i + 1, nums[i]);
        }
    }

    public void update(int index, int val) {
        add(index + 1, val- nums[index]);
        nums[index] = val;
    }

    public int sumRange(int left, int right) {
        return query(right + 1) - query(left);
    }

    private int lowbit(int x) {
        return x & -x;
    }

    private void add(int idx, int val) {
        for (int i = idx; i <= n; i += lowbit(i)) {
            tree[i] += val;
        }
    }

    // 前缀和
    private int query(int idx) {
        int ans = 0;
        for (int i = idx; i > 0; i -= lowbit(i)) {
            ans += tree[i];
        }
        return ans;
    }
}

线段树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
class NumArray {
    int[] nums;

    int[] tree = new int[100000];

    public NumArray(int[] nums) {
        this.nums = nums;
        buildTree(0, 0, nums.length - 1);
    }

    public void update(int index, int val) {
        update(0, 0, nums.length - 1, index, val);
    }

    public int sumRange(int left, int right) {
        return query(0, 0, nums.length - 1, left, right);
    }

    private void buildTree(int node, int start, int end) {
        if (start == end) {
            tree[node] = nums[start];
            return;
        }
        int leftNode = 2 * node + 1;
        int rightNode = 2 * node + 2;
        int mid = start + (end - start) / 2;
        buildTree(leftNode, start, mid);
        buildTree(rightNode, mid + 1, end);
        tree[node] = tree[leftNode] + tree[rightNode];
    }

    private void update(int node, int start, int end, int idx, int val) {
        if (start == end) {
            nums[idx] = val;
            tree[node] = val;
            return;
        }
        int leftNode = 2 * node + 1;
        int rightNode = 2 * node + 2;
        int mid = start + (end - start) / 2;
        if (idx >= start && idx <= mid) {
            update(leftNode, start, mid, idx, val);
        } else {
            update(rightNode, mid + 1, end, idx, val);
        }
        tree[node] = tree[leftNode] + tree[rightNode];
    }

    private int query(int node, int start, int end, int L, int R) {
        if (end < L || start > R) {
            return 0;
        }
        if (start >= L && end <= R) {
            return tree[node];
        }
        if (start == end) {
            return tree[node];
        }
        int leftNode = 2 * node + 1;
        int rightNode = 2 * node + 2;
        int mid = start + (end - start) / 2;
        int leftSum = query(leftNode, start, mid, L, R);
        int rightSum = query(rightNode, mid + 1, end, L, R);
        return leftSum + rightSum;
    }
}

线段树的tree数组的大小：

​ 设原数组长度为n，则线段树的树状数组一般声明为4*n